Предыдущее: "Определим орбиту двойной
Пробные частицы в двойной системе
Как бы двигались планеты Солнечной системы, если бы
рядом с Солнцем находилась вторая
звезда сравнимой массы? Теперь появляется уже не одна,
а две гравитационные воронки. Ясно, что такая система
должна быть гораздо сложнее. По-видимому, и Кеплеру
было бы трудно разобраться в таком движении.
Движение пробных частиц в поле тяжести двойной
звезды проще всего исследовать, перейдя в систему отсчета, жестко
вращающуюся вместе со звездами. Центр такой системы совмещен с центром масс, ось х направлена вдоль линии,
соединяющей звезды, ось у лежит в плоскости орбиты, а ось z
перпендикулярна к ней (рис. 10).
Так мы сможем избавиться от
вращения. Но избавившись от
вращения, мы приобретаем
центробежную силу, которая
возникает в любой неинерциальной системе отсчета. Но
это не страшно. В системах с
круговыми орбитами угловая
скорость обращения звезд по
орбите не меняется со временем : звезды движутся равномерно по окружностям.

Рис. 10Силы,
действующие на пробную частицу, не зависят от
времени,
а зависят только от положения частицы. Поэтому можно
пользоваться понятием потенциала.
В небесной механике такая задача называется ограниченной
задачей трех тел. Ограниченной, потому что
третье тело - пробная частица - не влияет на движение
двух других. В общем случае траектория частицы может
быть определена лишь численно, и по форме она будет
напоминать нечто, изображенное на рис. 10. Меняя начальные координаты
частицы и ее скорость, можно получить много траекторий такого типа. Число
разнообразных вариантов очень велико. Используя самые
совершенные вычислительные машины, мы можем сократить время счета, но при
этом " утонем " в том огромном
количестве промежуточной информации, которую нам будет выдавать машина.

К счастью, нам это не понадобится. Движение пробных
частиц можно исследовать качественно. При этом
не нужно следить за траекторией отдельной частицы.
Она настолько сложна, что это занятие совершенно бесполезное. Мы будем
следить лишь за судьбой частицы.
Впервые такое качественное исследование провел американский астроном и
математик Джордж Хилл в конце
прошлого века.
Пусть на пробную частицу действуют три силы: силы
притяжения от звезд М1 и М2
и центробежная сила. Все
эти силы потенциальные и могут быть описаны одним
эффективным потенциалом U. Давайте проследим за
частицей, движущейся в плоскости орбиты двойной.
Все три силы находятся в этой же плоскости, поэтому пробная частица никогда
из плоскости не выйдет.
Поведение потенциала U качественно показано
на
рис. 11. График представляет собой три "утеса", разделенных
воронками в том месте, где расположены звезды.
Сразу бросаются в глаза три особые точки. Положив
осторожно на вершины утесов пробные частички, мы заметим, что они так и
будут лежать в равновесии. Хоть
неустойчивом, но все же равновесии! Впервые эти точки
обнаружил великий французский ученый Луи Лагранж
в 1772 г.
Поверхности равного потенциала называются поверхностями
Хилла. Они получаются сечением потенциала
плоскостями, параллельными осям х и у (см. рис . 10).
А их проекции на плоскость ху показаны на рис.
11.
К сожалению, изобразить поведение потенциала в плоскости ху
непросто. Нужно иметь в виду, что на самом
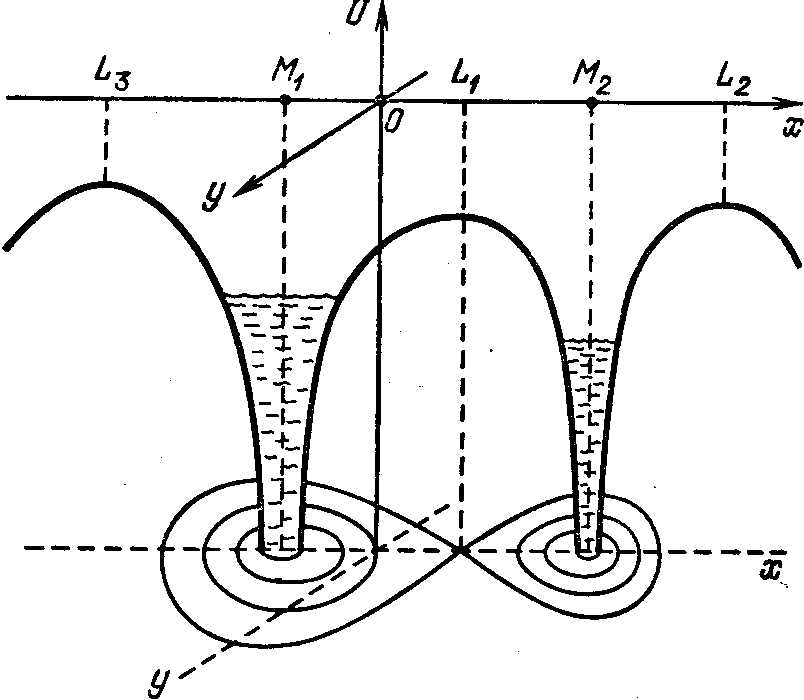
Рис. 11. Поведение эффективного потенциала в двойной
системе
деле потенциал нарастает при удалении от оси х
вдоль
оси у. Так что точки L1, L2 и
L3 это, скорее, не
вершины, а перевалы (см. рис. 12). Однако читатель может
заметить: если потенциал растет при удалении от точек
L1, L2 и
L3, а на бесконечности он опять мал, значит,
где-то есть вершины. Совершенно верно. Эти вершины
соответствуют еще двум точкам Лагранжа (иногда их называют точками
либрации). Но об этом мы поговорим чуть
дальше.

При движении пробной частицы сохраняется ее полная
энергия, т. е. сумма кинетической К и потенциальной U
энергии частицы:
К + U = E = const.
Поставим следующий мысленный эксперимент. Будем
запускать частички с одной из звезд. Очевидно, если мы
чуть-чуть подтолкнем частичку, то она немного поднимется вверх, а потом
опять свалится в воронку. В максимально удаленной от звезды точке частица
останавливается и ее кинетическая энергия обращается в нуль: К =
= 0. Значит, в этот момент полная энергия частицы
Е равна потенциалу в точке поворота. Понятно, что движение частицы
возможно только там, где U меньше или равно Е. Проведя
сечение потенциала по линии U = E, мы найдем область,
внутри которой могут двигаться частицы с энергией Е.
В трехмерии - это будут не линии, а поверхности равного потенциала
(поверхности Хилла). Таким образом
зная энергию частицы, мы можем указать зону ее дбижения.
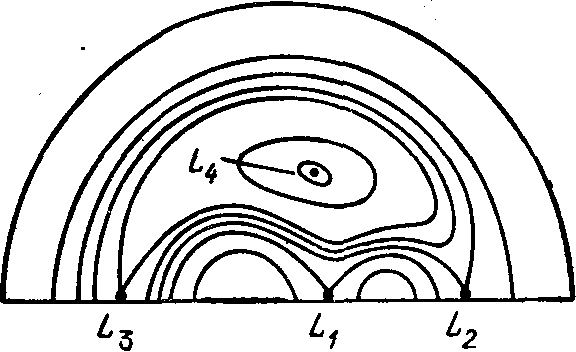
На рис. 13 показан
разрез поверхности Хилла,
в плоскости орбиты. Пока
энергия частицы мала,
мала и область возможного движения ее вокруг
звезды. "Выстреливая" частицы все с большей и
большей скоростью, мы
увеличиваем их энергию
и область их возможного
движения. При некотором
значении энергии области
сьежаются в точке Лагранжа L1 и
получается поверхность, похожая на
восьмерку. Ее
называют критической полостью Роша.
 Пробная частица, попавшая в точку L1, без затрат энергии
может попасть на соседнюю звезду. Частицы с очень большими энергиями могут
выйти за пределы полости Роша - они уже не принадлежат какой-то одной из
звезд. В точках Лагранжа равнодействующая всех сил, действующих на пробную
частицу, обращается в ноль. Читатель может воспользоваться последним
свойоством, чтобы найти положение этих точек/ Особенно просто отевт выглядит
в случае равных масс.
Пробная частица, попавшая в точку L1, без затрат энергии
может попасть на соседнюю звезду. Частицы с очень большими энергиями могут
выйти за пределы полости Роша - они уже не принадлежат какой-то одной из
звезд. В точках Лагранжа равнодействующая всех сил, действующих на пробную
частицу, обращается в ноль. Читатель может воспользоваться последним
свойоством, чтобы найти положение этих точек/ Особенно просто отевт выглядит
в случае равных масс.
Для эксцентрицных орбит движение пробных частиц уже не описывается
потенциальной функцией. И там уже нет никаких поверхностей Хилла и полостей
Роша и качественный анализ уже не проходит. Остается считать на компьютере.
Продолжение следует
Обозрение "Физические явления на небесах" профессора В.М.Липунова.
�